Một phiên bản của bài toán kinh điển về dãy Farey
21/12/2016  2
2
 24.939
24.939
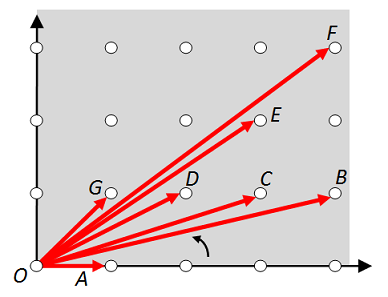
Lưới nguyên trên mặt phẳng bao gồm các điểm với cả hai toạ độ là các số nguyên. Một điểm của lưới nguyên gọi là nguyên sơ nếu đoạn thẳng nối nó với gốc toạ độ không chưa điểm nguyên nào khác.
Cho $A$ là một hình lồi chứa gốc toạ độ. Xếp các điểm nguyên sơ của lưới nguyên nằm trong $A$ lần lượt theo chiều kim đồng hồ nhìn từ gốc toạ độ. Đánh số chúng $x_1, x_2, \dots$
Cho B là một hình lồi chứa $A$ như tập con. Giả sử y là điểm nguyên sơ DUY NHẤT của lưới nguyên, ở trong $B$, nằm giữa $x_1$ va $x_2$ nếu nhìn từ gốc toạ độ.
Chứng minh rằng $ y=x_1+x_2 $.
Mới Nhất
- Thách thức kỳ này tập 8 - số 4 tháng 4.2024 - Ngày 01/04/2024
- Thách thức Toán học - Ngày 08/03/2024
- Thách thức Toán học - Ngày 27/02/2024
- Thách thức Toán học - Ngày 23/02/2024
Bình luận mới nhất (2) bình luận:
- HA THO : Bao giờ thì có lời giải vậy ad? - 17/02/2017
- Tuấn Lê Hoàng Anh : giá mà có thì hình ảnh thì sẽ dễ hiểu hơn đó ad ơi em khó hiểu quá - 12/02/2017








